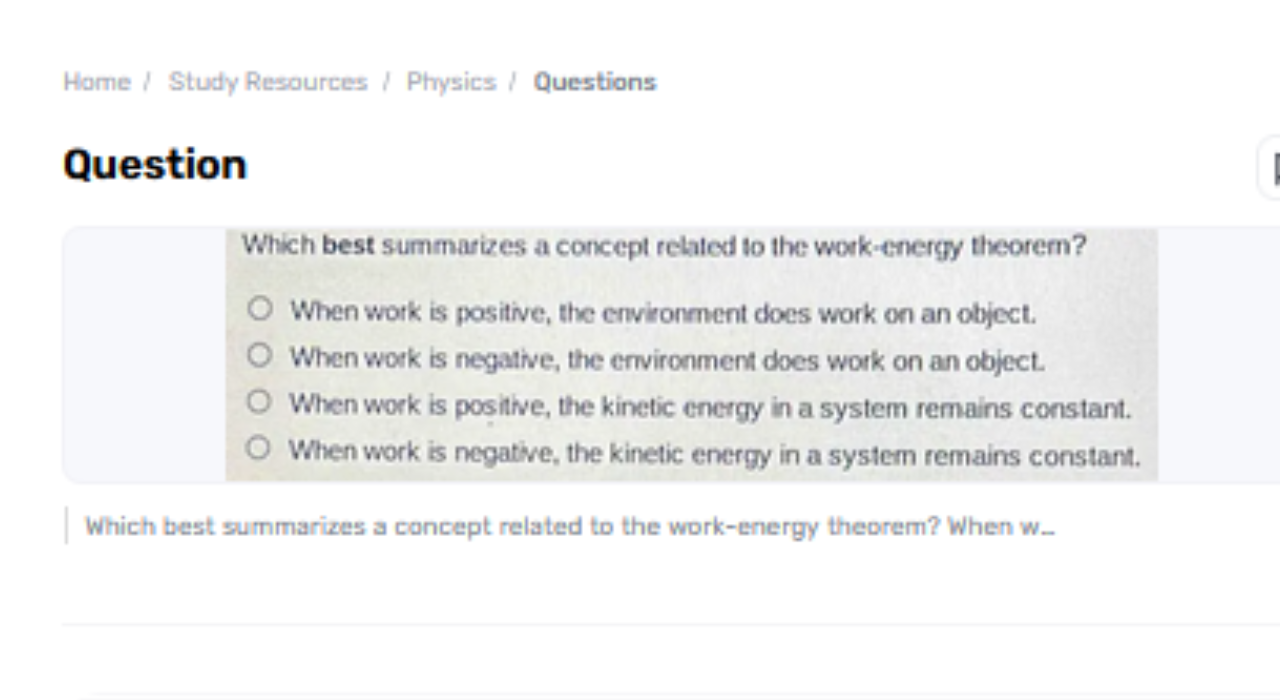
The work-energy hypothesis may be an essential rule in material science that sets up a coordinated relationship between the work done on a protest and the alteration in its motor vitality. This hypothesis gives pivotal bits of knowledge into how strengths impact the movement of objects, which best summarizes a concept related to the work-energy theorem? making it a foundation in classical mechanics. By understanding this concept, one can anticipate and analyze the impacts of different powers acting on objects and the coming changes in their motor vitality.
Understanding the Work-Energy Hypothesis: A Comprehensive Outline
The work-energy hypothesis interfaces the work done on a question to its alter in motor vitality, communicated as Wnet=KW_{text{net}} = Delta KWnet=K. This rule makes a difference analyze how powers change an object's movement, with applications extending from straightforward scenarios to complex frameworks, and bookkeeping for different real-world components.
The Work-Energy Hypothesis Characterized
The work-energy hypothesis states that the net work done by all powers acting on a question breaks even with the alteration in its motor vitality. Scientifically, it can be communicated as:
Wnet=ΔKW_{\text{net}} = \Delta KWnet=ΔK
where WnetW_{text{net}}Wnet speaks to the net work done, and ΔK\Delta KΔK signifies the alter in motor vitality. Motor vitality (KKK) is given by the condition:
K=12mv2K = frac{1}{2} mv^2K=21mv2
where mmm is the mass of the protest, and V is its speed. Agreeing with the hypothesis, on the off chance that a constraint acts on a question and causes it to quicken or decelerate, the work done by that force will specifically interpret into an alter within the object's active vitality.
Work Done by Strengths
Work done by a constraint is calculated as the product of the drive and the relocation of the protest within the heading of the drive. The scientific expression for work (WWW) is:
W=F⋅d⋅cos(θ)W = F \cdot d \cdot \cos(\theta)W=F⋅d⋅cos(θ)
where FFF is the size of the constrain, it is the relocation, and θthetaθ is the point between the constrain and the course of relocation. For a protest experiencing an alter in speed due to a constraint, the net work done consolidates all powers acting on the protest, counting grinding, gravity, and connected powers.
Gauth 3-Step Direct to Understanding Homework
1. Get it the Issue
Start by carefully perusing the homework task to get a handle on the concepts and necessities. Break down complex issues into smaller parts and distinguish key data, factors, and goals. On the off chance that fundamental, audit significant notes or course readings to clarify any instabilities.
2. Create a Arrange
Define a methodology to handle the issue based on the concepts and strategies you’ve checked on. Select fitting equations, procedures, or approaches and diagram the steps required to fathom the issue. This arrangement ought to incorporate organizing information, deciding calculations, and setting up conditions in case required.
3. Execute and Audit
Execute the arrangement by tackling the issue step-by-step, guaranteeing precision in calculations and coherent consistency. After arriving at an arrangement, audit your work to check for blunders and approve that the arrangement adjusts with the problem’s prerequisites. Make any essential rectifications and guarantee the ultimate reply is displayed.
Conclusion
In rundown, the work-energy hypothesis may be an essential guideline in material science that joins the work done on a protest to its alter in active vitality. By understanding this relationship, one can pick up profitable experiences into the impacts of different strengths on an object's movement. The theorem's application ranges a wide extend of scenarios, from straightforward cases of speeding up and deceleration to more complex frameworks with numerous strengths.